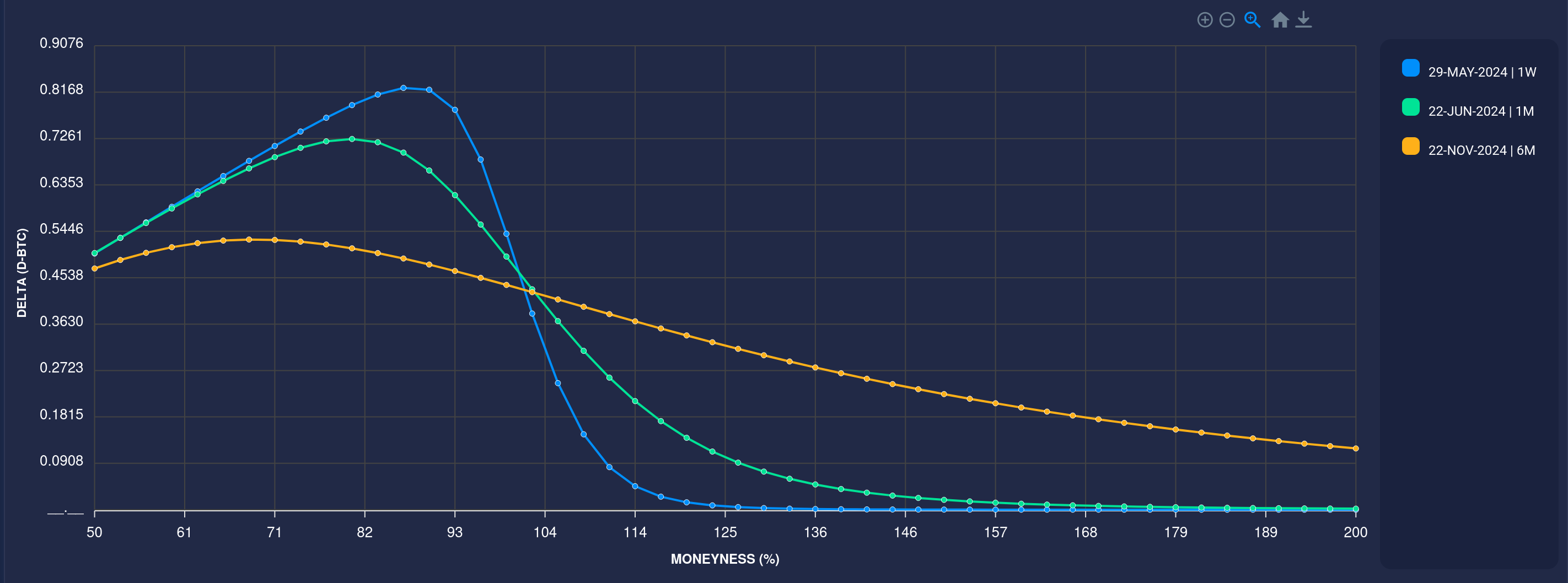
Pricing Crypto Options with a Flexible, API-Driven Approach
In our previous blog, we emphasized the importance of implied volatility for option traders and demonstrated how to retrieve it—across any strike scale and expiry—using a flexible API that:
- Supports a range of expiry definitions (tenor-based, listed, or custom date/time).
- Offers multiple strike scales (strike, moneyness, log-moneyness, delta call/put, or FX-style).
Transitioning from implied volatility to actual pricing requires the same versatile API—offering possibility to calculate these with different premium conventions (especially in FX or digital assets). In this post, we explore how to streamline pricing by:
- Allowing configurable premium conventions (for example, paying the premium in a chosen currency), and
- Defining preset payoffs that let users retrieve implied volatility, pricing, and risk metrics for multiple structures (European vanilla, digitals, risk reversals, strangles, ...) in one request.
Today, our focus is on European vanilla options as a straightforward example. The same method applies to more complex payoffs, which we’ll cover in future blogs.